Demostración del Área del Círculo mediante Integrales

Posted on by Ing. Domingo Fraga Hernandez

Este es mi primer artículo referente a una de mis materias favoritas de las matemáticas, el cálculo integral, con una de las demostraciones más interesante a mi parecer, el área de un círculo. En esta publicación, veremos la demostración del área de un círculo, sin ningún preámbulo comenzamos.

Área del Círculo

Representación Gráfica

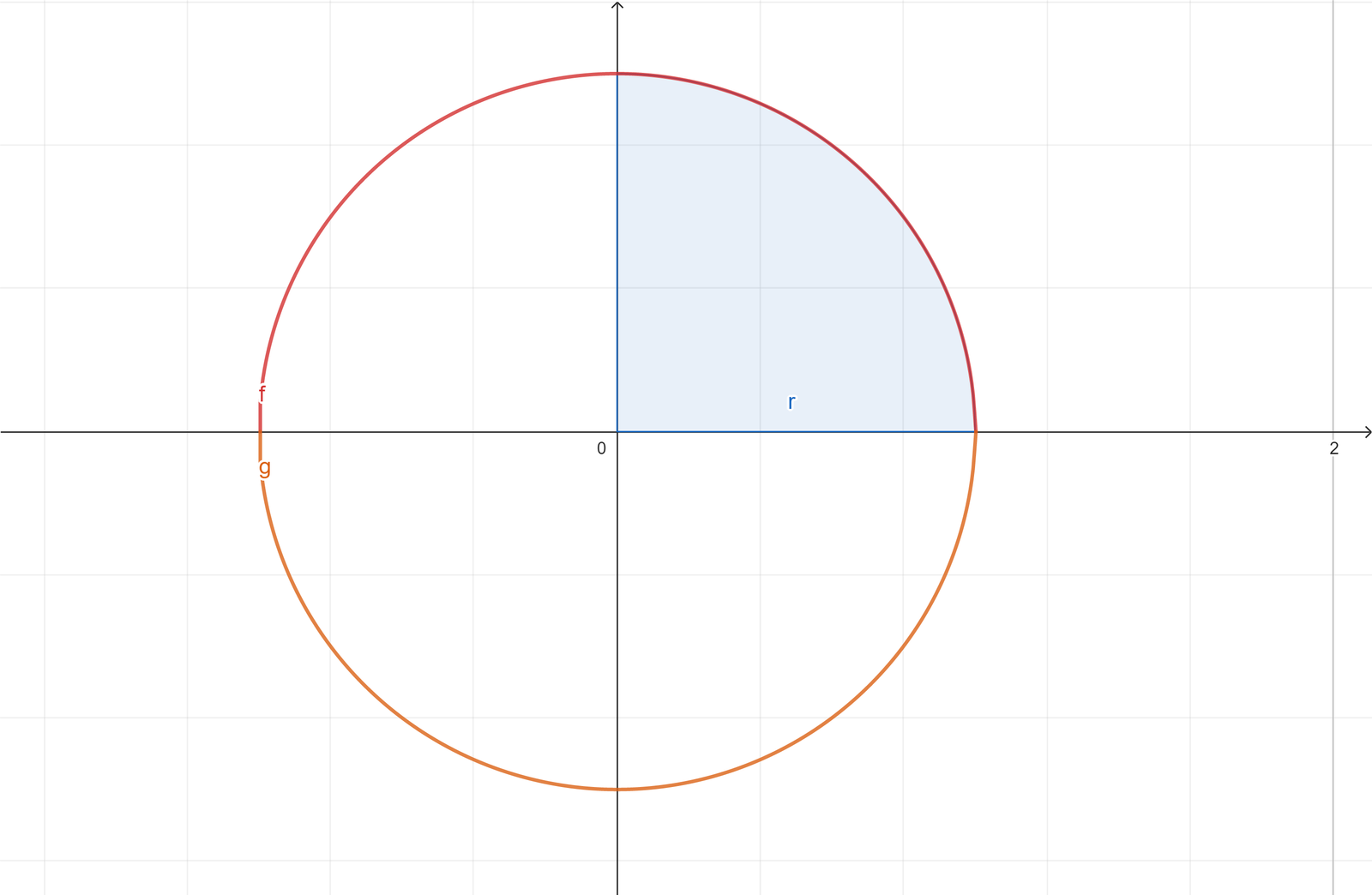
Sabemos que la ecuación del círculo es x^{2}+y^{2}=r^{2} ; así que despejaremos la y porque nos interesa integrarla como función y obtendremos la integral definida de 0 al radio \int_{0}^{r} \sqrt{r^{2}-x^{2}}\mathrm{d}x , la cual es el área en el primer cuadrante del plano cartesiano.

Comenzamos a calcular la integral, para resolverla utilizaremos la sustitución trigonométrica, obtenemos las sustituciones.

\sin{\alpha}=\frac{x}{r}\therefore x=r \sin{\alpha}\therefore \mathrm{d}x=r\cos{\alpha}\mathrm{d}{\alpha}\\ \cos{\alpha}=\frac{\sqrt{r^{2}-x^{2}}}{r} \therefore \sqrt{r^{2}-x^{2}}=r\cos{\alpha}

Calculamos los límites partiendo de las sustituciones obtenidas.

\alpha=\arcsin{\frac{x}{r}}\\ \alpha_{0}=\arcsin{\frac{0}{r}}=\arcsin{0}=0^{\circ}=0\\ \alpha_{r}=\arcsin{\frac{r}{r}}=\arcsin{1}=90^{\circ}=\frac{\pi}{2}

Aplicamos las sustituciones, en esta parte usaremos la identidad trigonométrica \cos^{2}{\alpha}=\frac{1}{2}\left(1+\cos{2\alpha}\right) .

\int_{0}^{\frac{\pi}{2}} \left(r\cos{\alpha}\right)\left(r\cos{\alpha} \mathrm{d}\alpha\right)\\ = r^{2}\int_{0}^{\frac{\pi}{2}} \cos^{2}{\alpha} \mathrm{d}\alpha\\ = r^{2}\int_{0}^{\frac{\pi}{2}}\frac{1}{2}(1+\cos{2\alpha}) \mathrm{d}\alpha\\ = \frac{r^{2}}{2}\int_{0}^{\frac{\pi}{2}} (1+\cos{2\alpha}) \mathrm{d}\alpha\\ = \frac{r^{2}}{2}\left(\int_{0}^{\frac{\pi}{2}} \mathrm{d}\alpha+\int_{0}^{\frac{\pi}{2}} \cos{2\alpha} \mathrm{d}\alpha\right)

Una vez aplicadas las sustituciones podemos comenzar a resolver.

\frac{r^{2}}{2}\left(\int_{0}^{\frac{\pi}{2}} \mathrm{d}\alpha+\int_{0}^{\frac{\pi}{2}} \cos{2\alpha} \mathrm{d}\alpha\right) \\\\ = \frac{r^{2}}{2}\left(\alpha \left.\right|_{0}^{\frac{\pi}{2}}+\int_{0}^{\frac{\pi}{2}} \cos{2\alpha} \mathrm{d}\alpha\right)\\ = \frac{r^{2}}{2}\left[\left(\frac{\pi}{2}-0\right)+\int_{0}^{\frac{\pi}{2}} \cos{2\alpha} \mathrm{d}\alpha\right]\\ = \frac{r^{2}}{2}\left(\frac{\pi}{2}+\int_{0}^{\frac{\pi}{2}} \cos{2\alpha} \mathrm{d}\alpha\right)

Nos detenemos en esta parte porque calcularemos la integral \int_{0}^{\frac{\pi}{2}} \cos{2\alpha} \mathrm{d}\alpha la cual podemos resolver mediante cambio de variable, comenzamos obteniendo las sustituciones.

u=2 \alpha\therefore \mathrm{d}u=2 \mathrm{d}\alpha \therefore \mathrm{d}\alpha=\frac{\mathrm{d}u}{2}

Calculamos los límites partiendo de las sustituciones obtenidas.

u=2 \alpha\\ u_{0}= 2(0)= 0= 0^{\circ}\\ u_{\frac{\pi}{2}}= 2\left(\frac{\pi}{2}\right)= \pi= 180^{\circ}

Retomamos el procedimiento aplicando las sustituciones.

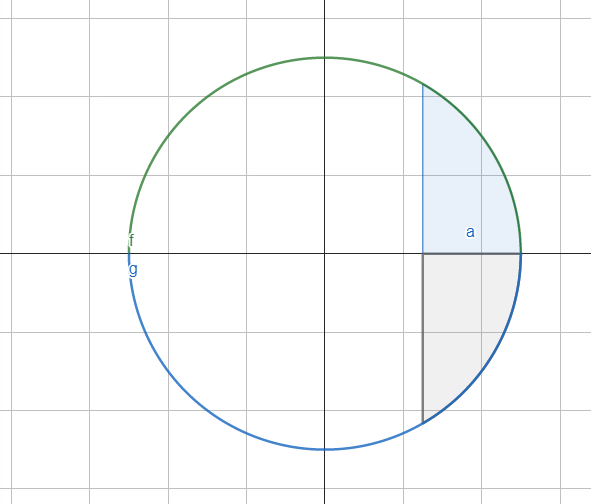
\frac{r^{2}}{2}\left[\frac{\pi}{2}+\int_{0^{\circ}}^{180^{\circ}} \cos{u} \left(\frac{\mathrm{d}u}{2}\right)\right]\\= \frac{r^{2}}{2}\left(\frac{\pi}{2}+\frac{1}{2}\int_{0^{\circ}}^{180^{\circ}} \cos{u} \mathrm{d}u\right)\\= \frac{r^{2}}{2}\left(\frac{1}{2}\centerdot\pi+\frac{1}{2}\int_{0^{\circ}}^{180^{\circ}} \cos{u} \mathrm{d}u\right)\\= \frac{r^{2}}{2}\centerdot\frac{1}{2}\left(\pi+\int_{0^{\circ}}^{180^{\circ}} \cos{u} \mathrm{d}u\right)\\= \frac{r^{2}}{4}\left(\pi+\int_{0^{\circ}}^{180^{\circ}} \cos{u} \mathrm{d}u\right)\\= \frac{r^{2}}{4}\left(\pi+ \sin{u}\left.\right|_{0^{\circ}}^{180^{\circ}}\right)\\= \frac{r^{2}}{4}\left[\pi+ \left(\sin{180^{\circ}}-\sin{0^{\circ}}\right)\right]\\= \frac{r^{2}\pi}{4}

El resultado es \frac{r^{2}\pi}{4} , ahora recordemos que es el área bajo la curva en un cuadrante del plano cartesiano, esto quiere decir que es la cuarta parte del área del círculo, por tanto, debemos multiplicar por 4 para obtener el área total, en su defecto \pi r^{2} .

El artículo ha concluido, dando comienzo a una nuevo tipo de contenido para el blog del cual procuraré traer más variedad, agradezco la atención prestada y espero que haya sido de utilidad mi aporte, cualquier comentario me lo puedes enviar y con gusto responderé.

Deja tus comentarios

Related Posts